Nhan

Solutions for the 2021 written examination 1.

Question 1

a. \(\dfrac{d}{dx}(2e^{-3x})\)

\[\dfrac{d}{dx}(2e^{-3x}) = 2 \dfrac{d}{dx}(e^{-3x})\]

Using the formula sheet, \(\dfrac{d}{dx}(e^{ax}) = ae^{ax}\). Here, \(a = -3\).

\[\begin{align} 2 \dfrac{d}{dx}(e^{-3x}) &= 2 \times -3e^{-3x} \\ &{} \textcolor{green}{ = -6e^{-3x} } \end{align}\]

b. \(f(x) = x \sqrt{2x + 1}\). Find \(f'(4)\).

Using the formula sheet, product rule \(\dfrac{d}{dx}(uv) = u \dfrac{dv}{dx} + v \dfrac{du}{dx}\). Here, \(u = x\) and \(v = (2x + 1)^\tfrac{1}{2}\). Using the formula sheet, \(\dfrac{d}{dx}( (ax + b)^n ) = an(ax + b)^{n-1}\) (a form of the chain rule).

\[\begin{align} f'(x) &= x \dfrac{d}{dx} \left( (2x + 1)^\tfrac{1}{2} \right) + (2x + 1)^\tfrac{1}{2} \dfrac{d}{dx}(x) \\ &= x \times 2 \times \frac{1}{2} \times (2x + 1)^{- \tfrac{1}{2} } + (2x + 1)^\tfrac{1}{2} \times 1 \\ &= \dfrac{x}{ \sqrt{2x + 1} } + \sqrt{2x + 1} \\ f'(4) &= \dfrac{4}{ \sqrt{2 \times 4 + 1} } + \sqrt{2 \times 4 + 1} \\ &{} \textcolor{green}{= \frac{13}{3} } \end{align}\]

Question 2

\(f'(x) = x^3 + x\) and \(f(1) = 2\). Find the rule of \(f(x)\).

Using the formula sheet, \(\displaystyle\int x^n dx = \dfrac{1}{n+1} x^{n+1} + c\).

\[f(x) = \frac{1}{4} x^4 + \frac{1}{2} x^2 + c\] \[\begin{align} f(1) &= 2 \\ \frac{1}{4} \times 1^4 + \frac{1}{2} \times 1^2 + c &= 2 \\ c &= \frac{5}{4} \end{align}\] \[\textcolor{green}{ f(x) = \frac{1}{4} x^4 + \frac{1}{2} x^2 + \frac{5}{4} }\]

Question 3

\(g: R \rightarrow R, g(x) = 2 \sin (2x)\)

a. State the range of \(g\).

For a function in a form \(a \sin \left( \dfrac{x}{b} \right)\), the range is \([-a, a]\). Here, \(a = 2\).

The range of \(g\) is

\[\textcolor{green}{[-2, 2]}\]

b. State the period of \(g\).

For a function in a form \(a \sin \left( \dfrac{x}{b} \right)\), the period is \(2 \pi b\). Here, \(b = \dfrac{1}{2}\).

The period of \(g\) is

\[\textcolor{green}{\pi}\]

c. Solve \(2 \sin (2x) = \sqrt{3}\) for \(x \in R\).

\[\begin{align} 2 \sin (2x) &= \sqrt{3} \\ \sin (2x) &= \frac{ \sqrt{3} }{2} \\ 2x &= 2 \pi n + \frac{\pi}{3}, 2 \pi n + \frac{2 \pi}{3} \text{ for } n \in Z \\ \textcolor{green}{x} &{} \textcolor{green}{ = \pi n + \frac{\pi}{6}, \pi n + \frac{\pi}{3} \text{ for } n \in Z } \end{align}\]

This general solution should confirm that the period of \(g\) is \(\pi\).

Question 4

a. Sketch \(y = 1 - \dfrac{2}{x-2}\).

The graph has a vertical asymptote \(x = 2\) as

\[\begin{align} y &= 1 - \frac{2}{2-2} \\ &= 1 - \frac{2}{0} \end{align}\]

is undefined.

The graph has a horizontal asymptote \(y = 1\) as

\[\begin{align} 1 &= 1 - \frac{2}{x-2} \\ \frac{2}{x-2} &= 0 \\ 2 &= 0 \end{align}\]

is impossible.

The graph has a y-axis intercept where \(x = 0\).

\[\begin{align} y &= 1 - \frac{2}{0-2} \\ &= 2 \end{align}\]

The y-axis intercept is at \((0, 2)\).

The graph has an x-axis intercept where \(y = 0\).

\[\begin{align} 0 &= 1 - \frac{2}{x-2} \\ x &= 4 \end{align}\]

The x-axis intercept is at \((4, 0)\).

The graph of \(y = 1 - \dfrac{2}{x-2}\) is below.

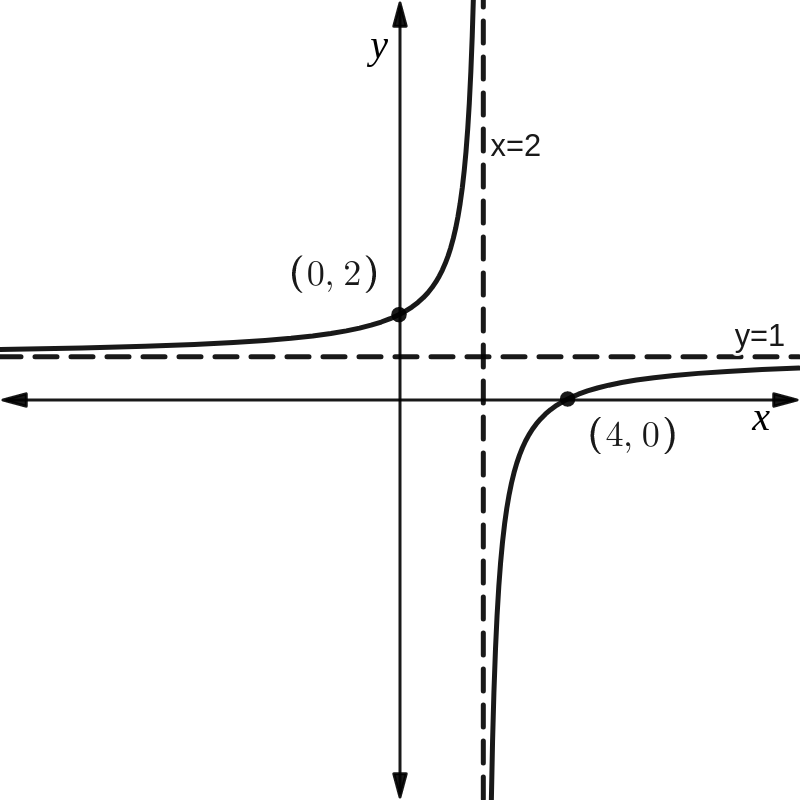
b. Find the values of \(x\) where \(1 - \dfrac{2}{x-2} \geq 3\).

\[\begin{align} 1 - \dfrac{2}{x-2} &= 3 \\ -2 &= \dfrac{2}{x-2} \\ -2x + 4 &= 2 \\ -2x &= -2 \\ x &= 1 \end{align}\]

From the graph,

\[\textcolor{green}{ x \in [1, 2) }\]

Question 5

\(f: R \rightarrow R, f(x) = x^2 - 4\) and \(g: R \rightarrow R, g(x) = 4(x - 1)^2 - 4\).

a. \(f\) and \(g\) both have a horizontal axis intercept at \((2, 0)\). Find the coordinates of the other horizontal axis intercept of \(g\).

\[\begin{align} g(x) &= 0 \\ 4(x - 1)^2 - 4 &= 0 \\ x &= 0, 2 \end{align}\] \[\textcolor{green}{(0, 0)}\]

b. \(h\) is \(f\) dilated by a factor of \(\dfrac{1}{2}\) from the vertical axis then translated \(2\) units right. Find the rule and the coordinates of the horizontal axis intercepts of \(h\).

\[\begin{align} x' &= \frac{1}{2} x + 2 \\ x &= 2(x' - 2) \end{align}\]

For the rule of \(h\):

\[\begin{align} h(x) &= f(2(x - 2)) \\ &= (2(x - 2))^2 - 4 \\ \textcolor{green}{h(x)} &{} \textcolor{green}{= 4(x - 2)^2 - 4} \end{align}\]

For the horizontal axis intercepts of \(h\):

\[\begin{align} h(x) &= 0 \\ x &= 1, 3 \end{align}\] \[\textcolor{green}{(1, 0), (3, 0)}\]

Note that \(h(x) = g(x-1)\), so the horizontal axis intercepts of \(h\) can be found also by translating the horizontal axis intercepts of \(g\) 1 unit right.

Question 6

A shop sells boxes of doughnuts. A doughnut can be glazed, have custard, neither, or both. A box contains 20 doughnuts. \(\dfrac{1}{2}\) have custard, \(\dfrac{7}{10}\) are not glazed, and \(\dfrac{1}{10}\) are glazed and have custard.

a. Find the probability that a doughnut taken at random from the box is not glazed and has custard.

Let \(G\) be the event that the doughnut is glazed, and \(C\) be the event that the doughnut has custard.

\[\begin{align} \mathrm{Pr}(G' \cap C) &= \mathrm{Pr}(C) - \mathrm{Pr}(G \cap C) \\ &= \frac{1}{2} - \frac{1}{10} \\ &{} \textcolor{green}{ = \frac{2}{5} } \end{align}\]

b. The 20 doughnuts are randomly allocated to boxes \(A\) and \(B\), which each now contain 10 doughnuts. Let \(g\) be the number of glazed doughnuts in box \(A\). A box and then a doughnut is chosen at random. Find the probability that the doughnut came from box \(B\) given that it is glazed, in terms of \(g\).

The number of glazed doughnuts overall is \(\left( 1 - \dfrac{7}{10} \right) \times 20 = 6\). The number of glazed doughnuts in box \(B\) is \(6 - g\).

\[\begin{align} \mathrm{Pr}(B|G) &= \frac{\mathrm{n}(B \cap G)}{\mathrm{n}(G)} \\ &{} \textcolor{green}{ = \frac{6 - g}{6} } \end{align}\]

c. The shop has many visitors, with \(\dfrac{1}{2}\) of these vistors less than 25 years old. \(\hat{P}\) is the random variable representing the proportion of visitors less than 25 years old from a random sample of 5 visitors. Find \(\mathrm{Pr}(\hat{P} \geq 0.8)\).

Let X be the random variable representing the number of visitors who are less than 25 years old in a random sample of 5 visitors, \(X \sim \mathrm{Bi} \left( 5, \dfrac{1}{2} \right)\).

Using the formula sheet, \(\hat{P} = \dfrac{X}{n}\). Here, \(n = 5\).

\[\begin{align} \hat{P} &= \dfrac{X}{5} \\ X &= 5 \hat{P} \end{align}\] \[\begin{align} \mathrm{Pr}(\hat{P} \geq 0.8) &= \mathrm{Pr}(X \geq 4) \\ &= \mathrm{Pr}(X=4) + \mathrm{Pr}(X=5) \\ &= \binom{5}{4} \left( \frac{1}{2} \right)^4 \left( \frac{1}{2} \right)^{5-4} + \binom{5}{5} \left(\frac{1}{2} \right)^5 \left(\frac{1}{2} \right)^{5-5} \\ &= 5 \left( \frac{1}{2} \right)^5 + 1 \left( \frac{1}{2} \right)^5 \\ &{} \textcolor{green}{ = \frac{3}{16} } \end{align}\]

Question 7

\(X\) is a random variable with probability density function \(f\)

\(f(x) = \left\{ \begin{array}{lr} \dfrac{k}{x^2} & 1 \leq x \leq 2 \\ \ 0 & \text{elsewhere} \end{array} \right.\)

a. Show that \(k = 2\).

For any probability density function, \(\displaystyle\int_{- \infty}^\infty f(x) dx = 1\). Using the formula sheet, \(\displaystyle\int x^n dx = \dfrac{1}{n + 1} x^{n + 1}\).

\[\begin{align} \int_1^2 k x^{-2} dx &= 1 \\ k \int_1^2 x^{-2} dx &= 1 \\ k \left[ -x^{-1} \right]_1^2 &= 1 \\ k(-2^{-1} + 1^{-1}) &= 1 \\ \textcolor{green}{k} &{} \textcolor{green}{= 2} \end{align}\]

b. Find \(\mathrm{E}(X)\).

Using the formula sheet, \(\displaystyle\int \dfrac{1}{x} dx = \log_e(x)\). Using the formula sheet, mean for a continuous probability distribution

\[\begin{align} \mathrm{E}(X) &= \mu \\ &= \int_{- \infty}^{\infty} x f(x) dx \\ &= \int_1^2 x \times \frac{2}{x^2} dx \\ &= \int_1^2 \frac{2}{x} dx \\ &= 2 \int_1^2 \frac{1}{x} dx \\ &= 2 [\log_e(x)]_1^2 \\ &= 2(\log_e(2) - \log_e(1)) \\ &{} \textcolor{green}{= 2 \log_e(2)} \end{align}\]

Question 8

The derivate of a function is \(\dfrac{dy}{dx} = \sqrt{x + 6} - \dfrac{x}{2} - \dfrac{3}{2}\). The function has a single stationary point \(\left( 3, \dfrac{29}{4} \right)\).

a. Find the rule of the function.

Using the formula sheet, \(\displaystyle\int (ax+b)^n dx = \dfrac{1}{a(n+1)} (ax+b)^{n+1} + c\).

\[\begin{align} y &= \int \frac{dy}{dx} dx \\ &= \int \left( (x+6)^\tfrac{1}{2} - \frac{x}{2} - \frac{3}{2} \right) dx \\ &= \frac{2}{3} (x+6)^\tfrac{3}{2} - \frac{1}{4} x^2 - \frac{3}{2} x + c \\ \end{align}\]

Substitute \((x, y) = \left( 3, \dfrac{29}{4} \right)\) into \(y = \dfrac{2}{3} (x+6)^\tfrac{3}{2} - \dfrac{1}{4} x^2 - \dfrac{3}{2} x + c\).

\[\begin{align} \frac{29}{4} &= \frac{2}{3} (3+6)^\tfrac{3}{2} - \frac{1}{4} \times 3^2 - \frac{3}{2} \times 3 + c \\ c &= -4 \end{align}\]

Substitute \(c = -4\) into \(y = \dfrac{2}{3} (x+6)^\tfrac{3}{2} - \dfrac{1}{4} x^2 - \dfrac{3}{2} x + c\).

\[\textcolor{green}{ y = \dfrac{2}{3} (x+6)^\tfrac{3}{2} - \dfrac{1}{4} x^2 - \dfrac{3}{2} x - 4 }\]

b. Determine the nature of the stationary point \(\left( 3, \dfrac{29}{4} \right)\).

Test for \(y\) or \(\dfrac{dy}{dx}\) using values of \(x\) either side of \(x = 3\).

We know that when \(x = 3\), \(y = \dfrac{29}{4}\) and \(\dfrac{dy}{dx} = 0\).

When \(x = -2\), \(y = \dfrac{10}{3}\) and \(\dfrac{dy}{dx} = \dfrac{3}{2}\).

When \(x = 10\), \(y = - \dfrac{4}{3}\) and \(\dfrac{dy}{dx} = - \dfrac{5}{2}\).

Note that \(y < \dfrac{29}{4}\) either side of \(\left( 3, \dfrac{29}{4} \right)\), or note that \(\dfrac{dy}{dx}\) changes sign from positive to negative at \(\left( 3, \dfrac{29}{4} \right)\).

The stationary point is a local maximum turning point.

Non-Methods method

Using the second derivative: at \( x = 3 \), \( \dfrac{d^2 y}{dx^2} = - \dfrac{1}{3} < 0 \).

Question 9

Consider the unit circle \(x^2 + y^2 = 1\), point \(O = (0, 0)\), point \(A = (2, 0)\), and point \(P\) on the unit circle. The tangent to the circle at point \(P\) is perpendicular to the line \(OP\), and passes through point \(A\).

a. Show that the equation of the line through points \(A\) and \(P\) is \(y = - \dfrac{x}{ \sqrt{3} } + \dfrac{2}{ \sqrt{3} }\).

Triangle \(AOP\) is a right-angled triangle with side lengths \(AO = 2\) and \(OP = 1\).

\[\begin{align} \cos(\angle AOP) &= \frac{OP}{AO} \\ &= \frac{1}{2} \\ \angle AOP &= \frac{\pi}{3} \end{align}\]

Using \(m = \tan (\theta)\), where \(m\) is the gradient of a line and \(\theta\) is the angle that the line makes with the positive direction of the horizontal axis. The line segment \(AO\) lies on the horizontal x-axis.

\[\begin{align} m_{OP} &= \tan(\angle AOP) \\ &= \tan \left( \frac{\pi}{3} \right) \\ &= \sqrt{3} \end{align}\]

Using \(m_1 m_2 = -1\), where \(m_1\) and \(m_2\) are the gradients of perpendicular lines. The lines \(AP\) and \(OP\) are perpendicular.

\[\begin{align} m_{AP} \times m_{OP} &= -1 \\ m_{AP} &= \frac{-1}{ m_{OP} } \\ &= \frac{-1}{ \sqrt{3} } \end{align}\]

Using \(y - y_0 = m(x - x_0)\), where \(m\) is the gradient of the line and \((x_0, y_0)\) is a point on the line. Here, \(m = \dfrac{-1}{ \sqrt{3} }\) and \((x_0, y_0) = (2, 0)\).

\[\begin{align} y - 0 &= \frac{-1}{ \sqrt{3} } (x - 2) \\ \textcolor{green}{y} &{} \textcolor{green}{ = - \frac{x}{ \sqrt{3} } + \frac{2}{ \sqrt{3} } } \end{align}\]

\(h\) is the line \(y = - \dfrac{x}{ \sqrt{3} } + \dfrac{2}{ \sqrt{3} }\) dilated by a factor of \(q\) from the x-axis, \(q \in R \setminus \{0\}\).

b i. Find the values of \(q\) for which \(h\) intersects the unit circle at least once.

The original line, \(h\) when \(q = 1\), touches the the unit circle once. The original line reflected in the x-axis, \(h\) when \(q = -1\), similarly touches the unit circle once. For \(q \in (-1, 1)\), \(h\) intersects the unit circle twice.

Note the restriction on \(q\).

\[\textcolor{green}{q \in [-1, 1] \setminus \{0\} }\]

b ii. \(h\) intersects the unit circle twice. Find the values of \(q\) for which the coordinates of the points of intersection of \(h\) and the unit circle have only positive values.

\(h\) intersects the unit circle twice when \(q \in (-1, 1)\). The y-coordinates of the points of intersection are positive when \(q > 0\).

The x-coordinates of the points of intersection are positive when the y-axis intercept of \(h\) is at \(y > 1\), otherwise one point of intersection will be at a non-positive x-coordinate. The y-axis intercept of the original line is at \(y = \dfrac{2}{ \sqrt{3} }\).

\[\begin{align} q \times \frac{2}{ \sqrt{3} } &> 1 \\ q &> \frac{ \sqrt{3} }{2} \end{align}\] \[\textcolor{green}{q \in \left( \frac{ \sqrt{3} }{2}, 1 \right)}\]

\(0 < q \leq 1\). \(P'\) is the point of intersection of \(h\) with the unit circle closest to \(A\) and \(\theta\) is the angle \(\angle AOP'\). \(g\) is a function of \(\theta\) giving the area of the triangle \(OAP'\).

c i. Define the function \(g\).

From part a., when \(q = 1\), \(\theta = \dfrac{\pi}{3}\).

\[\begin{align} 0 &< q \leq 1 \\ 0 &< \theta \leq \frac{\pi}{3} \end{align}\]

To find the rule of \(g\), we have two methods.

Method 1

Using the formula sheet, area of a triangle is \(\dfrac{1}{2} bc \sin(A)\). Here, \(b = 2\), \(c = 1\), and \(A = \theta\).

\[\begin{align} g(\theta) &= \frac{1}{2} \times 2 \times 1 \times \sin(\theta) \\ &= \sin(\theta) \end{align}\]

Method 2

Using area of a triangle is \(\dfrac{1}{2} \times base \times height\). Here, \(base = 2\) and \(height\) is the y-coordinate of \(P'\) which is \(\sin(\theta)\) as \(P'\) lies on the unit circle.

\[\begin{align} g(\theta) &= \frac{1}{2} \times 2 \times \sin(\theta) \\ &= \sin(\theta) \end{align}\] \[\textcolor{green}{g: \left( 0, \frac{\pi}{3} \right] \rightarrow R, g(\theta) = \sin(\theta)}\]

c ii. Find the maximum possible area of the triangle \(OAP'\).

\(g(\theta)\) is increasing for its entire domain \(\theta \in \left( 0, \dfrac{\pi}{3} \right]\). \(g(\theta)\) is at its maximum when \(\theta = \dfrac{\pi}{3}\).

\(g \left( \dfrac{\pi}{3} \right) \textcolor{green}{ = \dfrac{ \sqrt{3} }{2} }\) square units